Clicking the above logo will bring you to a Swedish thrash metal band, rather than mysterious cryptograms. Nevertheless, you may find yourself puzzling over their indecipherable lyrics.
Here is another quick (and pointless) diversion. As explored in the previous post, you can find words in the cryptograms without performing any substitutions. For example, in the 408-character cryptogram, the word “OUT” appears:
And the word “RIDE” can be discerned:
If we apply the solution key to those “words”, we get:
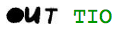
This led me to a question: Using the cipher symbols, can we create any “words” that turn into valid plain text words when deciphered using the 408’s solution key?
The tools I built for the previous post were still lying around, so they were useful in satisfying this nagging curiosity. Turns out that many words can be made this way. In the sampling below, each plaintext word is followed by its encipherment using the 408’s key. Then the interpretation of the encipherment is shown:
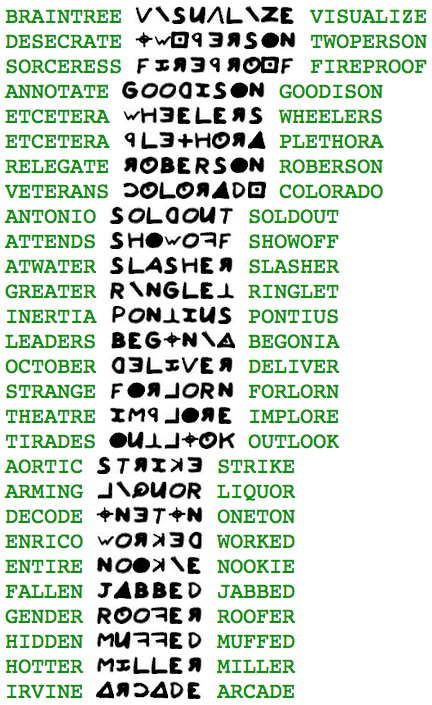
(If you really want to challenge your brain, try to find a word whose encipherment’s word can itself be enciphered into yet another valid word.)
One reason I was curious about these “word pairs” was because of the possibility that Zodiac “seeded” his solution key with a keyword. But even if he did, it seems impossible to discover the keyword, since too many words can be found by chance. Here’s another example of how easy it is to draw out ridiculous outcomes solely from chance:
Among the symbols of the 408-character cryptogram, Zodiac includes the normal looking letters A through Z, but excludes C. So, let’s write out those cipher letters, with the corresponding plain text substitutions underneath:
Now we can re-arrange the assignments to look for keywords:
Surely “the buffoon’s sweet genitalia” is not the message Zodiac was trying to convey…
Many people have noticed that words can be found among the symbols in the Zodiac killer’s cryptograms without performing any substitutions. Here are some examples from the 340:
HER 
TOM 
Looks a lot like “ZODIAC” 
FBI 
TOO 
GOD |
BOO is seen three times 
BOY is found twice |
Five occurrences of BY, resembling the Halloween card |
And here are some words easily found in the 408:
(more…)
Between 1956 and 1981, math and science writer Martin Gardner wrote the Mathematical Games
Some of Gardner’s wonderful puzzles, games, and curiosities.
He even wrote a book about codes and ciphers
I recently found an index to a collection of Martin Gardner’s correspondences and notes at Stanford University, and was surprised to discover that some of them pertain to the Zodiac ciphers. Naturally, I had to order photocopies and have a look.
Among the collection are letters that writer and amateur sleuth Gareth Penn wrote to Gardner in 1981 and 1984. Those who follow the Zodiac case have probably heard of Gareth Penn, a man who, for over twenty years, has obsessively written reams of material with bizarre theories linking UC Berkley professor Michael O’Hare to the Zodiac killings. Penn’s fixations have also drawn suspicions that he himself is the Zodiac killer. For a better background on this fascinating example of misplaced obsession, read “With Malice Aforethought” by Michael Martin, and Michael O’Hare’s own responses to the whole affair.
In his first letter to Gardner, Penn writes about how much he enjoys Gardner’s column on mathematical puzzles, and encloses copies of his various articles and writings about the Zodiac Killer:
(more…)
(photo credit: Elonka Dunin)
Thanks to Doc for informing me about this story. Above is CIA analyst David Stein, the first person to crack encrypted messages in the Kryptos sculpture at the CIA, leaving only one message unsolved. Twenty-three years after the sculpture was created, the last message still remains unsolved.
Wired.com posted this story recently, triggered by the NSA widely distributing Stein’s declassified and fascinating account of how he tackled Kryptos for over seven years using only pen and paper. Although Stein was first, his work was only known to CIA colleagues. Cryptographer and computer scientist Jim Gillogly was the first to publicly announce the correct solutions, but he was unaware of Stein’s work. Gillogly is also known for identifying a strange sequence in one of the Beale cryptograms, which he explains is evidence that the Beale papers are a hoax.
Read more about how Stein cracked Kryptos here. And be sure to read Elonka Dunin’s nicely organized breakdown of the entire Stein article. Those of us working on the 340 might find some insight and new ideas in such details.
Mike Morford recently relaunched his Zodiac Killer discussion forum:
His forum was formerly available by invitation only, but is now open to everyone. It is filled with lively conversations on a wide variety of topics, including news, suspects, the killer’s correspondences, evidence, analysis, theories, and non-Zodiac crimes. My favorite topics, of course, are the cipher-related ones, in which forum members present their ideas, observations, and theories about the various cryptograms attributed to the killer.
Join the conversation at ZodiacKillerSite.com!
On October 23, 1969, the San Francisco Examiner published an article about the ongoing hunt for the Zodiac killer. This enciphered “message to Zodiac” appeared in the article:
The article was published after the 408-character cryptogram was solved, and before the 340-character cryptogram was mailed.
Using a simple observation, you can easily solve the Examiner’s cryptogram (if you want to skip ahead to the solution, click here). The cryptogram has only 44 characters, and 33 of them are unique. With so few repeated characters, many possible plain texts can fit. For example, if you feed the cryptogram to zkdecrypto, it yields this plaintext:
ERSWILLYOURAGESTOFTHECANAMEDTHEPRESANDBEINTE
This solution looks a lot like English text, but is the wrong solution. This cryptogram would have been very difficult to solve without applying the simple observation. Do you know of a way to solve it without knowing the trick?
(Thanks to Deb for uncovering the article)
UPDATE Apr 24, 2013: Here is an excerpt from the book The Cases That Haunt Us
Updated April 17, 2013: In light of recent events, I’ve decided to remove the ricin recipe plaintext from this post. The FBI, however, continues to display the encrypted ricin recipe on their website.
Cryptographer Klaus Schmeh recently posted about a cryptogram that appears in an FBI article about how their Cryptanalysis and Racketeering Records Unit (CRRU) breaks codes and ciphers to solve crimes.
The FBI article says the cryptogram contains “enciphered instructions for making ricin poison found in the notebook of a lone bomber in Virginia.” I couldn’t find any decryptions of the cipher text, so I transcribed it, and fed it into zkdecrypto lite, which very quickly found a rough approximation of the plaintext. A little bit of extra work yielded the full solution, which really does contain a recipe for ricin poison, encrypted using simple homophonic substitution.
At first I was hesitant to post the solution. Is it irresponsible to reveal a dangerous recipe to the public? But I’ve decided to post it for these reasons:
- The FBI already posted the cryptogram in full view of the public.
- The cryptogram is very easy to solve.
- Ricin recipes are already very easy to come by via Google searches.
- The enciphered recipe is very crude, producing only a mash form that is not further purified for dangerous potential. Similar recipes in terrorist “cookbooks” are “deemed incapable of achieving a good product for causing a large number of casualties by any exposure route, mainly because of the low content of toxin of the final extracts” [1]
- Only one death has been attributed to ricin poisoning. Every other ricin-related incident seems to involve dumbasses stockpiling the stuff for its claimed deadly potential.
Here’s the decoded plaintext:
[redacted]
And here is the full analysis of the solution, including the solution key, symbol cycles, and symbol frequencies.
The cryptogram bears some interesting similarities to the Zodiac’s ciphers: It is 354 characters long (to Zodiac’s 340), has 65 distinct symbols (to Zodiac’s 64 in the 408-character cipher), uses homophonic substitution (like Zodiac’s 408), and uses some of the same symbols. The ricin bomber, however, did not do a good job of concealing the letter frequencies of the plaintext. In fact, if you look at the symbol frequencies, the most common symbols correspond directly to the most common letters in English: E, T, A, O, N, etc. This is because the lone bomber did not correctly flatten the frequencies with the proper number of symbol assignments per plain text letter.
The FBI says this cryptogram is just one small part of 24 pages of enciphered messages. It would be interesting to see what else was in the notebook, and to know more about the bomber. I can’t find any news sources that mention the Virginia lone bomber. Does anyone have any ideas?
Dan Johnson recently posted a really curious discovery about the 340-character cipher on his blog. First, number each of the positions of the cipher from 1 to 340. Then, mark each of the positions occupied by a 
symbol, the most common symbol, appearing 24 times in the cipher. You’ll get this list of numbers:
- 20, 40, 64, 65, 72, 81, 105, 128, 133, 140, 142, 159, 162, 172, 201, 211, 237, 238, 255, 276, 282, 290, 291, 340
Then, mark every number that is a prime number. Recall from your math classes that a prime number is a number greater than 1 that can’t be divided by anything other than 1 and itself. Here’s the result of marking the primes in the above list:
- 20, 40, 64, 65, 72, 81, 105, 128, 133, 140, 142, 159, 162, 172, 201, 211, 237, 238, 255, 276, 282, 290, 291, 340
There’s only one prime number in the list. Dan points out that 20% of the numbers between 1 to 340 are primes, so we should expect more of the symbols to fall upon prime positions simply by chance. Yet only one does. Is this just a coincidence, or is it some reflection of the cipher author’s method?
I ran an experiment similar to Dan’s, using a computer program that randomly places symbols and counts how many primes they fall upon. First, it scrambles the 340 cipher into a random order, like shuffling a deck of cards. Then it counts how many symbols fall upon prime positions. The result is that out of 1,000,000 random shuffles, only 28,877 of them have exactly 0 or 1 symbols falling upon prime positions. That’s about 2.9% of all the shuffles.
That result can be interpreted like this: Let’s say you were creating a 340-character cipher, and you need to place 24 copies of a particular symbol. If you didn’t care at all about whether or not they were placed on primes, then you’d have about a 2.9% chance of avoiding all but one prime position.
So, it’s possible that the cipher’s author accidentally produced this oddity simply by placing the symbols. A 2.9% chance isn’t rare enough to rule out pure coincidence, but it’s certainly curious.
However, Dan goes on further to point out that 
, the 2nd most frequent symbol in the 340 cipher, occurs 12 times and yet also only falls on a single prime position:
- 21, 35, 147, 168, 181, 203, 216, 240, 261, 286, 315, 319
The symbols and account for 10% of all of the symbols of the 340 cipher, and yet only fall on two primes.
I repeated the “random shuffle” experiment, counting how often and 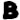each fall on no more than one prime. The experiment confirmed Dan’s result: Only 0.7% of the shuffles accidentally shared the same quality as the original 340 cipher.
Strange, isn’t it?
What about Zodiac’s previous cipher? Does it show this same strangeness?
The 408 cipher’s most common symbols are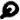 
(found 16 times), 
(found 14 times),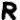 
(found 12 times), 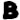(found 12 times), and 
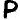(found 11 times). Three of those symbols fall on non-prime positions all but one time: , 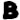and 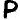. Those three symbols account for about 9% of the entire cipher text.
Repeating the shuffle test for the 408, I found only 1.8% of the 1,000,000 shuffled 408-character ciphers had this same quality.
Why would the cipher symbols be biased against prime positions? Is there something to this, or are we just chasing noise again?
One way to explore the idea further is to simulate the construction method of the 408 cipher. A computer program could generate a million different real ciphers, using different plain texts and somewhat regular sequences of homophones. Then the program can measure how many of the generated ciphers accidentally have these strange prime properties. Perhaps there is some link between the regular assignment of homophone sequences (or some other aspect of the cipher construction), and the probability that the symbols will fall upon primes.
If the ciphers really are prime-phobic, can this knowledge help us unravel the 340?
German computer scientist and cryptology writer Klaus Schmeh recently published a German-language book about famous unsolved secret messages, including the Zodiac Killer cryptograms.
(The cover depicts what we all probably want to do with Zodiac’s cryptograms.)
Nicht Zu Knacken
Relying on Google Translate, I tried to digest the chapter on the Zodiac Killer. Klaus first gives a brief summary of the crimes, including a timeline of the letters and codes. He also relates the story of the Hardens’ successful decryption of the 408-character cryptogram. The Hardens were not cryptography experts, but they knew enough about cryptograms to understand the importance of English letter frequencies in attacking substitution ciphers. They also knew the importance of trying out cribs in the cipher text, which successfully revealed other pieces of the plain text. Klaus describes the effect the Hardens’ success had on them. Reportedly, Bettye Harden had trouble dealing with all of the sudden attention and fame, and developed a manic-depressive personality disorder.
Here are some of the other bits of info Klaus mentions:
- Donald Harden was asked to work on the 340-character cryptogram, but refused. However, Bettye “barricaded herself in her room for weeks” to try to solve it, but failed. The CIA and NSA also failed to crack the code.
- The 13-character cryptogram is very difficult to solve, because it is too short for cryptanalysis.
- The Zodiac Killer case went cold in the late 1970s, but then started to heat up again as the Internet became widespread in the late 1990s, and sites such as Tom Voigt’s Zodiackiller.com appeared.
- Robert Graysmith points out in his book “Zodiac
” several cryptography books that were available at the time of the crimes: “The Codebreakers
” by David Kahn, and “Codes and Ciphers
” by John Laffin.
The 340 is still of interest to cryptographers because of its length. The 13 and 32 character cryptograms are simply too short, making definitive solutions very unlikely. But the 340 is long enough to hold out hope for a definitive solution resulting from discovery of an encryption scheme.
Based on symbol frequencies, Klaus observes that the 340 has some homophonic properties (letters in the hidden message might be represented by multiple symbols), suggesting a construction similar to the 408. But he wonders if the same method was used a second time. Since the 408 was solved so quickly, Zodiac could have changed his method, perhaps by adding meaningless letters, or by completely changing his encryption technique.
Homophonic substitution ciphers make decryption difficult, but not impossible, as the Hardens demonstrated. Failing with cribs, one could try to guess common letter pairs. But the 340 does not have much to work with. Another strategy is to look at the homophone order (the sequences of symbols assigned to individual plaintext letters).
While researching his book, Klaus met Austrian Mensa member Jürgen Koller, who was developing his own method of detecting homophone usage in the Zodiac ciphers. His “two-time repetition” approach can be found here. And his Austrian Mensa article about the Zodiac ciphers can be found on page 36 in this “Top IQ” Mensa journal published last year.
Klaus also mentions the Cryptologia paper by John King and Dennis Bahler, An Algorithmic Solution of Sequential Homophonic Ciphers. The method described in the paper is very powerful for attacking cryptograms that are constructed with sequential homophones. You can see the pattern of sequential homophones in this detailed breakdown of the solution to the 408. The 408 is easily cracked by King and Bahler’s method, but no solution is found for the 340 using the same method. I believe the same regularities that make ciphers like the 408 vulnerable to King and Bahler’s technique also make them easily cracked by hillclimbing computer programs such as zkdecrypto.
But the Zodiac killer probably did something unique to the 340 to make it withstand attacks from these various methods. Homemade test ciphers that are 340-characters long and share the same symbol distribution easily fall to these assorted attacks. I don’t think we can keep assuming that a simple substitution attack will work. Something else is probably going on in the encryption scheme in the 340. Or it’s just pointless busywork which continues to hypnotize us nearly a half century after it was created.
What is the “something else” the killer might have applied to the 340-character cryptogram? Klaus mentions Robert Graysmith’s “solution”, but points out the overuse of unusual abbreviations, misspellings, and incomprehensible wording. Those traits are common when you allow anagramming in your approach to the solution (you can see many examples of them here). Klaus also notes Raymond Grant, whose book “The Zodiac Murders – Solved” describes elaborate hidden messages in the Zodiac letters, and is “simply too confusing to be true” and “more of a curiosity than a serious contribution.” Many more ideas have been explored. Hopefully one of them will lead to a breakthrough.
Overall, Klaus Schmeh’s book is very interesting. It goes a bit beyond the usual “Top Unsolved Codes” lists that occasionally appear in the news to tease our thirst for mysteries. Brush up on your German and visit Klaus’ blog in which he unearths more mysteries and tidbits. And watch his appearance on German TV show “Planet Knowledge” during a full hour-long episode about secret codes.
Recent Comments