Are the ciphers prime-phobic?
Dan Johnson recently posted a really curious discovery about the 340-character cipher on his blog. First, number each of the positions of the cipher from 1 to 340. Then, mark each of the positions occupied by a  symbol, the most common symbol, appearing 24 times in the cipher. You’ll get this list of numbers:
symbol, the most common symbol, appearing 24 times in the cipher. You’ll get this list of numbers:
- 20, 40, 64, 65, 72, 81, 105, 128, 133, 140, 142, 159, 162, 172, 201, 211, 237, 238, 255, 276, 282, 290, 291, 340
Then, mark every number that is a prime number. Recall from your math classes that a prime number is a number greater than 1 that can’t be divided by anything other than 1 and itself. Here’s the result of marking the primes in the above list:
- 20, 40, 64, 65, 72, 81, 105, 128, 133, 140, 142, 159, 162, 172, 201, 211, 237, 238, 255, 276, 282, 290, 291, 340
There’s only one prime number in the list. Dan points out that 20% of the numbers between 1 to 340 are primes, so we should expect more of the  symbols to fall upon prime positions simply by chance. Yet only one does. Is this just a coincidence, or is it some reflection of the cipher author’s method?
symbols to fall upon prime positions simply by chance. Yet only one does. Is this just a coincidence, or is it some reflection of the cipher author’s method?
I ran an experiment similar to Dan’s, using a computer program that randomly places symbols and counts how many primes they fall upon. First, it scrambles the 340 cipher into a random order, like shuffling a deck of cards. Then it counts how many  symbols fall upon prime positions. The result is that out of 1,000,000 random shuffles, only 28,877 of them have exactly 0 or 1
symbols fall upon prime positions. The result is that out of 1,000,000 random shuffles, only 28,877 of them have exactly 0 or 1  symbols falling upon prime positions. That’s about 2.9% of all the shuffles.
symbols falling upon prime positions. That’s about 2.9% of all the shuffles.
That result can be interpreted like this: Let’s say you were creating a 340-character cipher, and you need to place 24 copies of a particular symbol. If you didn’t care at all about whether or not they were placed on primes, then you’d have about a 2.9% chance of avoiding all but one prime position.
So, it’s possible that the cipher’s author accidentally produced this oddity simply by placing the symbols. A 2.9% chance isn’t rare enough to rule out pure coincidence, but it’s certainly curious.
However, Dan goes on further to point out that 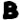 , the 2nd most frequent symbol in the 340 cipher, occurs 12 times and yet also only falls on a single prime position:
, the 2nd most frequent symbol in the 340 cipher, occurs 12 times and yet also only falls on a single prime position:
- 21, 35, 147, 168, 181, 203, 216, 240, 261, 286, 315, 319
The symbols  and
and 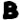 account for 10% of all of the symbols of the 340 cipher, and yet only fall on two primes.
account for 10% of all of the symbols of the 340 cipher, and yet only fall on two primes.
I repeated the “random shuffle” experiment, counting how often  and
and 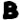 each fall on no more than one prime. The experiment confirmed Dan’s result: Only 0.7% of the shuffles accidentally shared the same quality as the original 340 cipher.
each fall on no more than one prime. The experiment confirmed Dan’s result: Only 0.7% of the shuffles accidentally shared the same quality as the original 340 cipher.
Strange, isn’t it?
What about Zodiac’s previous cipher? Does it show this same strangeness?
The 408 cipher’s most common symbols are 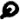 (found 16 times),
(found 16 times),  (found 14 times),
(found 14 times), 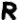 (found 12 times),
(found 12 times), 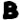 (found 12 times), and
(found 12 times), and 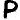 (found 11 times). Three of those symbols fall on non-prime positions all but one time:
(found 11 times). Three of those symbols fall on non-prime positions all but one time:  ,
, 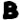 and
and 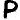 . Those three symbols account for about 9% of the entire cipher text.
. Those three symbols account for about 9% of the entire cipher text.
Repeating the shuffle test for the 408, I found only 1.8% of the 1,000,000 shuffled 408-character ciphers had this same quality.
Why would the cipher symbols be biased against prime positions? Is there something to this, or are we just chasing noise again?
One way to explore the idea further is to simulate the construction method of the 408 cipher. A computer program could generate a million different real ciphers, using different plain texts and somewhat regular sequences of homophones. Then the program can measure how many of the generated ciphers accidentally have these strange prime properties. Perhaps there is some link between the regular assignment of homophone sequences (or some other aspect of the cipher construction), and the probability that the symbols will fall upon primes.
If the ciphers really are prime-phobic, can this knowledge help us unravel the 340?
I worked on the “prime” approach about six months ago, and I too noticed the anomaly with the “+” symbol and prime numbers. Unfortunately, I was stumped after that (as always with the 340). I did not notice the “B” and prime aversion, though.
Please keep us updated! Always exciting to read news on this site!
Doc