Deborah Silva recently purchased from Tom Voigt a police photograph of the map code letter the Zodiac Killer mailed to the SF Chronicle on June 26, 1970. She generously shared this high quality scan of the photograph:
(Click to enlarge)
Thanks, Deborah!
The May 21, 2011 issue of New Scientist ran a feature called “Uncrackable Codes”, which featured MacGregor Campbell’s summaries of eight famous unsolved mysteries: Somerton Man, Beale’s buried treasure, the MIT time-lock puzzle, Kryptos, the Voynich Manuscript, Enigma, Elgar’s unread message, and the Zodiac Killer.
The Zodiac feature doesn’t have any new details, but here are some highlights:
- “In November 1969, Zodiac sent a code to the local papers that law-enforcers still believe could hold the key to solving the case.” This seems like wishful thinking. Cracking the 408 didn’t catch the killer. But maybe this wish will come true.
- FBI crypto chief Dan Olson says the 340 “is number one on his unit’s internal ‘top 10’ list of unsolved codes”, and that that he gets about 20 to 30 submissions every year from the public. None have led to breakthroughs.
- FBI cryptanalysts believe the 340 contains a real message, since the distribution of characters in the rows is not equal to the distribution of characters in the columns. Olson describes this in more detail in the emails he sent to Tom Voigt back in 2009.
- In 2009, computer scientist Ryan Garlick led his students in an attempt to use genetic algorithms to crack the cryptograms. The attempt was successful for the 408, but not the 340.
- Another attempt at San Jose State University also failed to produce a solution for the 340.
- Garlick thinks to crack the 340, its symbols need to be rearranged somehow. But he says figuring out the rearrangement is very difficult: “You have to happen upon exactly the right thing before any of our software tools would even get close.”
These kinds of “Top Unsolved Codes” lists appear from time to time, and usually only contain the briefest summaries of the mysteries. The MIT time-lock puzzle is one I haven’t seen before. And it was nice to see in the Zodiac feature a summary of academic attempts to crack the codes. How many other places in academia have been working on the dusty old Zodiac ciphers? The ones that I’ve come across include:
- Kevin Knight et. al at the University of Southern California
- Nuhn, Schamper and Ney at RWTH Aachen University, Germany
- Michael James Banks at the University of York
- Raddum and Sys from universities in Norway and Slovakia
- King and Bahler via Hewlett-Packard and North Carolina State University
All the research seems to be centered on attacking the 340 as if it is a simple substitution cipher. Most papers report succeeding at breaking the 408 and failing with the 340. I’ve yet to see any academic research into the idea of rearranging the 340’s symbols, or exploring its other qualities that might offer clues into how it is truly constructed. This seems to point to falsifying the hypothesis that the 340’s plain text is written in valid English, arranged in a normal direction, and enciphered using straightforward homophonic substitution. My guess is that exploring all the strange variations that are possible would result in tools that are too specific to apply to other “pen and paper” style ciphers. A lot of work for potentially zero reward. Who’s up to the challenge?
Audrey Cooper, managing editor of the San Francisco Chronicle, recently tweeted this:
The thickness of that stack of papers suggests lengthy and convoluted attempts to justify the claimed solution. It’d be interesting to know what approach the solver took. In the photo, the letter starts by discussing the cycling of variants (also known as homophones) in the 408:
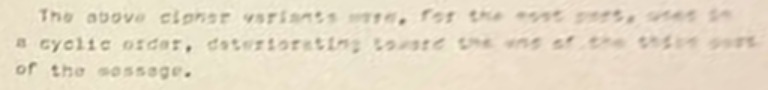
The above cipher variants were, for the most part, made in a cyclic order, deteriorating toward the end of the third part of the message
The letter shows the key, with all the variants (homophones) displayed beneath each plain text letter:
Then there’s a breakdown of the key, showing normal-looking alphabetic cipher symbols first, followed by the symbols that look like backwards letters, and then the symbols that look like shapes and punctuation:
The letter writer points out the interesting fact that “LMN” happens to decode to “THE”.
So far, the letter is off to a reasonable and logical start. I wonder where it leads.
The file of solution claims at the Chronicle must be massive. Reporter Kevin Fagan once told me they still get about two submissions per week. It’d be interesting to look at the file to see all the different approaches people have taken, and to find out how many of them fall into the usual traps, and if any of them supply new and useful ideas.
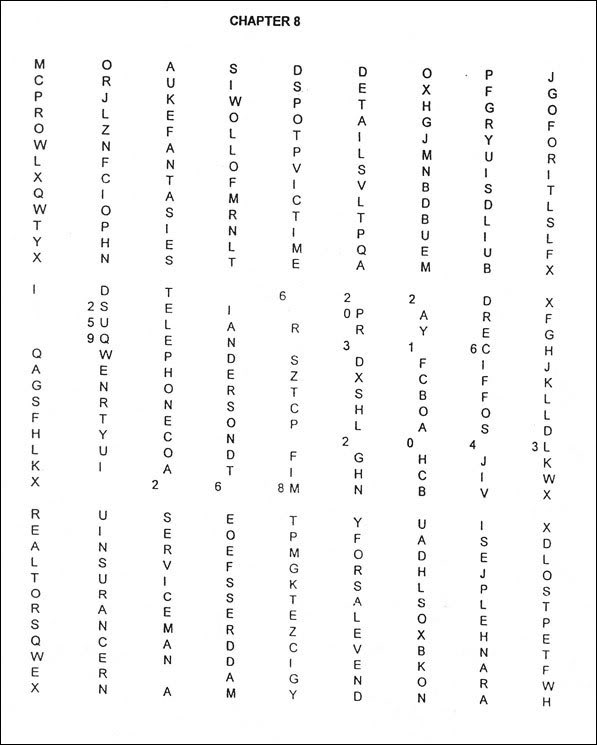
The 13-character cryptogram mailed by Zodiac on April 20, 1970 to the San Francisco Chronicle remains unsolved, despite many attempts to find solutions that fit into the cipher text.
Did Zodiac really encipher a name in this letter? If we assume that the cipher is a simple substitution cipher, read from left to right, then it is difficult to find real names that fit. This is because only 8 of the 13 symbols are unique. The repeated symbols are:
: Occurs 3 times.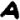
: Occurs 2 times.
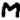: Occurs 2 times.
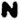: Occurs 2 times.
Assuming that each of those symbols can only represent one plaintext letter, many names we try to plug in will fail, because they will violate the cipher’s constraints.
We can roughly estimate the probability of 13 characters of plain text fitting into the cipher text. First, we start with these event probabilities:
- Probability of two letters repeating in English (p2): About 0.0655.
- Probability of three letters repeating in English (p3): About 0.00535.
Since we must have three identical letters, AND three sets of identical pairs, we must multiply the probabailities of each event together:
p3 * (p2)3 = 1.5 x 10-6, or about 1 in 670,000
Another way to look at this is to consider all possible 13-letter plain texts. Each position can be one of 26 letters, so that means for 13 spots there are 2613 possible plain texts (about two quintillion). But there are only 8 different symbols in the cipher, which means there are really only 268 possible plain texts (about 200 billion). That means that only about 1 in 12,000,000 plain texts will fit into the cipher without violating its constraints.
I found a database of a hundred million person names and wrote a program that scans them to look for names that fit in the cipher. When examining a name, the program allows the first, middle, and last names to appear in different orders, and allows any of the name parts to be abbreviated with initials. It discards anything that isn’t exactly 13 letters long. This results in almost a half billion tests of name combinations. The algorithm found only 213 plain texts that fit the cipher text. That works out to about 1 hit for every 2,000,000 attempts. Here is a sampling of the more interesting names that fit:
(more…)
Like Zodiac, serial killer Dennis Rader, also known as BTK, taunted police and newspapers with letters boasting of his crimes.
Among the many correspondences was a word puzzle Rader sent to Wichita television station KAKE on May 5 of 2004 [1] [2], shown here:
It was not difficult for people to find several words relevant to Rader’s crimes, such as:
(more…)
The Association for Computational Linguistics held its 2013 conference in Bulgaria earlier this month. Computational Linguistics is the study of how to apply computer science to problems involving language and speech. It’s a very broad subject, which also includes studies of how to decipher codes and cryptograms.
An interesting paper to emerge from this conference is “Beam Search for Solving Substitution Ciphers”, authored by some folks from RWTH Aachen University in Germany. They claim the technique in their paper can very quickly crack substitution ciphers with very small decipherment error. They also apply the technique to the Zodiac Killer’s 408-character cryptogram.
The paper has this claim:
Unlike the previous state-of-the-art approach that uses additional word lists to evaluate possible decipherments, our approach only uses a letter-based 6-gram language model.”
They must not be aware of other effective n-gram based hillclimbers such as zkdecrypto and CryptoCrack. This is probably because those tools are seldom cited in other academic papers, so researchers tend to overlook them.
(Ravi and Knight, 2011a) report the first automatic decipherment of the Zodiac-408 cipher. They use a combination of a 3-gram language model and a word dictionary.
From the referenced paper:
The new method can be applied on more complex substitution ciphers and we demonstrate its utility by cracking the famous Zodiac-408 cipher in a fully automated fashion, which has never been done before.
An early version of zkdecrypto was able to automatically and fully decipher the 408 back in December 2006. My 2008 paper descibes an automatic decipherment of enough of the 408 to easily derive the complete solution. And there must be other automatic solvers out there that could have handled the job. The 408 is not a difficult cryptogram to solve using statistical methods, because there are enough clues in it to give codebreakers leverage.
This small oversight notwithstanding, the new approach described in the ACL 2013 paper is interesting. Beam search is a variation of breadth-first search. A breadth-first search starts with an initial key, and then explores every possible change to it. This is not practical, due to the astronomical number of possible keys. Beam search fixes that by “pruning out” the low-scoring possibilities, so it only has to explore the ones it thinks are worth the trouble. The scores are based on n-gram statistics, weeding out solutions that don’t resemble normal English.
This seems to be a bit more systematic than other hillclimbers such as zkdecrypto that use a randomized search that continually “perturbs” the key, exploring the higher-scoring modifications. It’s unclear how well beam search stacks up against zkdecrypto, since zkdecrypto is already shown to be very fast and effective. The paper does not mention the unsolved 340 at all. The 340 will very likely not succumb to yet another approach that assumes a conventional construction, but I’m still curious what happened when they ran the algorithm against it.
Also in the conference, Kevin Knight gave a tutorial entitled “Decipherment”, in which he discussed the basics of codebreaking, classic historical ciphers, and famous unsolved codes:
Click here to view the slides from his tutorial
Highlights:
- An interesting angle Knight presents is that translating from a foreign language is a lot like dealing with a cipher, where you substitute words with other words.
- This slide made me think of zkdecrypto:
Random restarts are used in zkdecrypto to great effect, helping the hillclimbing search avoid getting stuck on hills that are too small. - Knight reviews some recent historical decipherments: Jefferson cipher, a Civil War cryptogram, German Naval Enigma, and Knight’s own work cracking the Copiale cipher.
- One of the keys to cracking the Copiale cipher was to cluster the cipher alphabet based on similar contexts (i.e., certain symbols tend to be preceded by or followed by specific symbols). The clusters were determined with a very useful “cosine similarity” measurement, which I implemented in CryptoScope. If you switch to the 408 there, and click the “Letter Contacts” button, you’ll see a Cosine similarities section under the contacts grid. It shows how all the real homophones tend to cluster at the top of the list.
- I’d assumed that much of the Copiale breakthroughs were discovered via computer, but apparently a lot of pencil and paper work was needed:
- The NSA recently declassified a 1979 paper by Mary D’Imperio about applying modern statistical techniques to the Voynich Manuscript. See also: D’Imperio’s The Voynich Manuscript: An Elegant Enigma.
- The NSA also recently declassified 4,400 pages of its newsletter, “Cryptolog“. Despite containing numerous redactions, it has some interesting articles on many topics, including the Voynich Manuscript.
- Knight talked about his 2011 paper with Ravi in which their method produced a very accurate decipherment of the Zodiac’s 408 cipher.
- He also talked about the unsolved Zodiac 340, and how it has no obvious reading order bias based on analyzing bigrams in several directions:
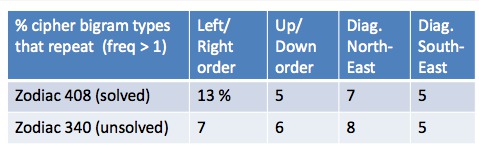
There you can see the 408 has a preference for left/right order, since it results in a spike of repeating bigrams. So, the 340 “could be nonsense, or maybe bigrams are smoothed out via more careful substitutions.”
Sounds like it was a fascinating conference. Maybe I can attend the next one. Meanwhile, have a look at the NSA’s upcoming 2013 Cryptologic History Symposium. Among the speakers will be Klaus Schmeh and David Kahn. And I’ve heard that Elonka Dunin will be there. Looks like a unique learning opportunity!
Here’s a fun, but arguably pointless gadget I built as a follow up to the article about ambiguous word searches:
Click here to try out the Word Search Gadget
You enter a word, click the search button, then the gadget hunts through the cipher text for the word. Symbols are interpreted directly as normal letters, and the letters have to be next to each other in the cipher text. Sometimes you can find words that appear in straight lines (HER, BOO, GOD, ZODAIK, etc.) Other times the words are folded up in different directions (BOMB, DOOR, PENTOBARBITONE).
Here are some details about how to work the controls:
Enter your search here. Then fiddle with the other settings, or just click on the Search button to accept the defaults.
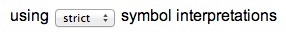
The search interprets symbols two different ways: strictly, and loosely. If you choose “strict”, then only these normal-looking letters and flipped letters are interpreted:
If you choose “loose”, then these extra rotations and manipulations are also considered:
Selecting “loose” will usually find more matches, since the search will force many symbols to look like other letters.
The search will match words that wander in different directions. You can limit the number of changes in direction by entering a new number here. For example, if you only want to match words that appear in perfectly straight lines, then enter “0” here.
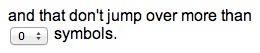
By default, the search requires that all letters are right next to each other in any direction. But you can modify the search here to allow for some “jumps”, or skipped symbols. Here is an example of the word “KILL” found by allowing at least two jumps:
Be careful with this setting, because sometimes it makes the search take too long, which may make your browser unresponsive for a little while.
Shuffling the cipher text is a way to test how easily words can appear by pure chance alone. When you click the “Shuffle” button, the cipher text is shuffled like a deck of cards until your word is found. It will stop after 1,000 shuffles if your word isn’t found.
After clicking the “Search” button, any results are displayed here. The “permalink” link gives you a way to bookmark the current search. Here are some sample permalinks: POINTYBEARD, DECIPHER, PARADICE, MALEIDENTIFIED, WELLROTTED, and MARTYR.
This part of the results shows you how the symbols are interpreted. Any strongly ambiguous symbols are manipulated to clarify how they are interpreted.
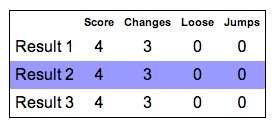
In this list of results, the highlighted result is shown in the cipher text grid to the left. You can see different results by moving your mouse cursor over different rows of the table.
Each result is shown with a score and some other values. “Changes” shows how many direction changes were required to find the word. “Loose” is a count of how many loose interpretations were needed to find the word. “Jumps” indicates how many times a symbol had to be skipped to complete the word. These are combined into the “Score” which is a way to estimate the quality of the result. Lower scores are better, and they are shown at the top of the list.
At the bottom of the cipher grid, you can click these buttons to switch between the 340 and 408 ciphers.
What words can you find? Leave them in the comments!
“EPotts” on Tom’s forum posted this intriguing observation about the names of the Zodiac Killer’s victims:
May be nothing but I noticed names like FErrin-EDwards-STein-BAtes-yet only 2 out of the top 100 most common surnames have letters in alphabetical sequence like this. Maybe just a coincidence? I think it could be but thought I would mention it. sorry if this has been posted b4
Confirmed victims Darlene Ferrin and Paul Stein have last names that begin with two letters that are adjacent in the alphabet. Unconfirmed victims Linda Edwards and Cheri Jo Bates do also.
Let’s look at all the victim names. There are reportedly seven confirmed victims: David Arthur Faraday, Betty Lou Jensen, Michael Renault Mageau, Darlene Elizabeth Ferrin, Bryan Calvin Hartnell, and Paul Lee Stine. There are at least four unconfirmed victims: Robert Domingos, Linda Edwards, Cheri Jo Bates, and Donna Lass (five if you include Kathleen Johns). People often debate over these lists but let’s go with the ten names for now.
As it turns out, if you pick ten last names completely at random, there’s about a 1.3% chance that at least four of them will have this interesting pattern. (If you want to torture yourself by seeing the math behind this, click here.)
Seems very rare, doesn’t it? Did the killer select his victims because of this pattern in their last names?
Well, maybe. But we have to be careful here. We know that the chances of finding this particular interesting pattern are low. But we didn’t consider other interesting patterns.
For instance, what if 4 out of the 10 names start with the same letter? Or if they end with letters that are adjacent in the alphabet? Or if each name starts and ends with the same letter? If we were looking at another list of names, and it had one of these other kinds of patterns, would we think it was significant?
For that reason, we need to change the question from:
- What are the odds this interesting pattern happens completely by chance?
to:
- What are the odds any interesting pattern happens completely by chance?
To demonstrate this, click here to run an experiment that shows how patterns can be found in random names. When you click the button there, it will select 10 names at random from the 30,000 most common names in this US census data. The random selections are done 1,000 times. The experiment then displays any sets of names that matched at least four patterns.
By default, it only looks for the kind of pattern EPotts discovered. Now, let’s see what happens when we include more kinds of patterns. Click more of the checkboxes to select more patterns, then click the button again. You’ll see that more matches are displayed. In fact, if you select every checkbox, then around 40% of the random trials will result in interesting patterns.
With some creativity, we could think of even more kinds of patterns that would stand out in a list of names. For example, what if the first letters of each name anagrammed to another name or interesting word? If such a pattern is discovered in a list of names, surely it would seem too unlikely to occur by random chance. But when all such patterns are considered, the odds are quite high that we’ll find something interesting.
If the Zodiac killer really did select victims whose names formed a pattern, we’d need some stronger evidence to show that it was intentional. What if all of the victim names followed EPotts’ pattern? If they did, the odds of it happening by chance drop from 1.3% to 0.0000000001%, which is very compelling. But they don’t, so we’d need more proof, such as some other direct reference to the scheme, perhaps among Zodiac’s correspondences.
WARNING: Here comes the boring math part.
As mentioned earlier, if you pick ten last names completely at random, there’s about a 1.3% chance that at least four of them will have this interesting pattern. How can we figure this out directly, instead of running an experiment to estimate the odds?
If you look at the census data, about 1 of every 10 names have EPott’s pattern. So we can say that there’s a 10% chance than any name will have it.
When we pick random names, we are filling 10 empty spots:
After filling the slots, let’s say we found 4 names that have the pattern, and 6 that don’t. We show names with the pattern as green, and the rest as red:
What is the probability of this exact arrangement of slots happening? Take a moment and think of a six-sided die. The probability of rolling a 2 is 1/6. The probability of rolling a 4 is 1/6. What is the probability of first rolling a 2, and then rolling a 4? Answer: 1/6 * 1/6 = 1/36.
Similarly, the probability of a green slot is 1 in 10. The probability of a red slot is 9 in 10. To figure out the probability for all slots, we multply the probabilities: (1/10) * (1/10) * (1/10) * (1/10) * (9/10) * (9/10) * (9/10) * (9/10) * (9/10) * (9/10) = 0.0000531441.
That tiny number is the probability of that one event happening. But there are more ways that four green slots can appear. They can be in different positions:
And there could be more than four green slots:
Again, think about the six-sided die. What is the probability of rolling a 3? Answer: 1/6. What is the probability of rolling a 3 OR rolling a 5? Answer: 1/6 + 1/6 = 1/3.
Similarly, we must add the probabilities for each of the possible events where at least 4 green squares appear. How many arrangements of the slots have at least 4 green squares? We have to use combinatorics to get the answer.
The number of ways to choose 4 slots from 10 is “10 choose 4”, or C(10,4), which is 210.
So, we have to add that tiny probability 210 times. Thus the probability that selecting 10 random names will result in exactly 4 green slots and 6 red slots is: 210 * 0.0000531441 = 0.011160261 (or 1.12%).
But we aren’t quite done yet. We also have to include situations where there are exactly 5 green slots, or 6 green slots, or 7 green slots, etc.
The probability that one particular event has:
- Exactly 4 green slots and 6 red slots: (1/10)4 * (9/10)6 = 0.0000531441
- Exactly 5 green slots and 5 red slots: (1/10)5 * (9/10)5 = 5.9049 × 10-6
- Exactly 6 green slots and 4 red slots: (1/10)6 * (9/10)4 = 6.561 × 10-7
- Exactly 7 green slots and 3 red slots: (1/10)7 * (9/10)3 = 7.29 × 10-8
- Exactly 8 green slots and 2 red slots: (1/10)8 * (9/10)2 = 8.1 × 10-9
- Exactly 9 green slots and 1 red slots: (1/10)9 * (9/10)1 = 9 × 10-10
- Exactly 10 green slots and 0 red slots: (1/10)10 * (9/10)0 = 1 × 10-10
Now we have to count all the ways for those events to happen:
- Ways for exactly 4 green slots and 6 red slots to appear: C(10, 4) = 210
- Ways for exactly 5 green slots and 5 red slots to appear: C(10, 5) = 252
- Ways for exactly 6 green slots and 4 red slots to appear: C(10, 6) = 210
- Ways for exactly 7 green slots and 3 red slots to appear: C(10, 7) = 120
- Ways for exactly 8 green slots and 2 red slots to appear: C(10, 8) = 45
- Ways for exactly 9 green slots and 1 red slots to appear: C(10, 9) = 10
- Ways for exactly 10 green slots and 0 red slots to appear: C(10, 10) = 1
Then, to get the total probability that at least 4 green slots will appear among 10 random selections, we multiply the counts by the corresponding probabilities, and then add them all up:
Total probability =
210 * 0.0000531441 +
252 * 5.9049 × 10-6 +
210 * 6.561 × 10-7 +
120 * 7.29 × 10-8 +
45 * 8.1 × 10-9 +
10 * 9 × 10-10 +
1 * 1 × 10-10 = 0.0128 (or 1.28%).
My apologies if these explanations are as cryptic as the ciphers!
Over on the ZodiacKillerSite forums, pi is doing some interesting work investigating the use of route patterns in quadrants of the 340-character cipher.
His idea is to split the cipher text into four quadrants, and then rearrange the text in each quadrant based on all of the possible routes. He then measures the resulting cipher text to see if more repeating patterns emerge from the text, with the hope that the underlying rearrangement has more features of a real message.
What he found was that running this search on the 340 increases the repeating patterns in at least 15% of his tests. By contrast, doing the same search on the 408 only increases the patterns 0.0000076% of the time. I found a similar phenomenon when exploring quadrants with a slightly different approach (see here and here).
But this led to more questions: What would happen to other 340-character test ciphers? How hard is it to make a 340-character cipher that has very few repeated patterns, yet still contains a valid message?
To answer this, pi created a test cipher that contains very few repeated patterns.
This means the repeated pattern count alone is not enough to separate good and bad rearrangements. What can we use instead? Dan’s approach avoids measuring the candidate cipher text altogether by skipping directly to trying to solve the rearranged text via the zkdecrypto hillclimber. It is a slow approach, but methodical. But is there some measurement that we can apply as a short cut? I think this is still an open question, and that we still need to generate more test ciphers to answer it.
Does the 340 cipher contain simple manipulations that have confounded all attempts to crack it? Dan Umanovskis, the skilled programmer who hacked together zkdecrypto-lite, has created a new kind of attack to explore this possibility. Using a genetic programming approach, his new algorithm evolves manipulations of the cipher text, such as swapping rows, removing columns, and flipping the text. The algorithm then feeds the modified cipher text to zkdecrypto-lite which hunts for readable plain text. Candidate manipulations that result in higher zkdecrypto scores are kept (“survival of the fittest”) and “bred” (mixed together) to look for even better scores.
Hopefully his approach will bear fruit. Even if it doesn’t find a solution to the 340, it can be used to exclude certain possibilities. For instance, you can create many test ciphers that resemble the 340 and contain the types of manipulations that the algorithm searches for. If the algorithm can successfully crack all the test ciphers, and no solutions are appearing for the 340, then it’s likely the 340 uses some other method of encryption.
You can download and play with Dan’s algorithm here: https://github.com/umanovskis/lgp-decrypto, and read Dan’s description here: http://www.zodiackillerfacts.com/forum/viewtopic.php?f=50&t=1537.
Recent Comments