Lafferty vs the ciphers
Retired Vallejo officer Lyndon Lafferty has been getting a lot of attention for his book in which he claims to know who the Zodiac killer was. The numerous criticisms of his claims aren’t mentioned by the various news stories, but you can find them here, here, here, here, here, and here.
Lafferty claims to have solved the unsolved Zodiac ciphers, but fails to provide details on his solutions. Like many of his other claims, he expects you to take his word for it. To make matters worse, instead of sharing the solutions outright, he says he intends to profit from them:
The detailed explanation and analysis, including the unbelieveable and undeniable pattern, will be offered for sale at the first opportunity.
Would you pay him?
Well, here’s a taste of his code work: I recently received a copy of his attempted solution to the unsolved 13-character “My name is” cipher. Lafferty appears to take as many liberties in his code work as he does in his book. Let’s look at how he shoehorns his suspect, William Joseph Grant, into the cipher.
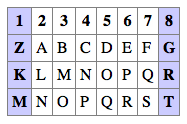
Here’s the 13-character “My name is” cipher text:


 symbols as shift operators. The shift is performed on the symbols immediately preceding them:
symbols as shift operators. The shift is performed on the symbols immediately preceding them:  (Z), K, and M.
(Z), K, and M.




NAME GRANT

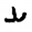 symbol is the astrological sign for “Aries”, or the “Ram”, and substitutes the symbol with those words. The words “ARE” and “IS” can be found in “Aries”, and “Ram” can be re-arranged to “MAR” (Grant was born in March). I’m going to ignore this step for now, so we can focus on how Lafferty generated a name out of the cipher text.
symbol is the astrological sign for “Aries”, or the “Ram”, and substitutes the symbol with those words. The words “ARE” and “IS” can be found in “Aries”, and “Ram” can be re-arranged to “MAR” (Grant was born in March). I’m going to ignore this step for now, so we can focus on how Lafferty generated a name out of the cipher text.
His decryption process is very convoluted. Does that by itself make it wrong? Not necessarily. But convoluted solutions tend to have many problems. My rule of thumb for verifying solutions is: Can other reasonable solutions be generated from the same process? If so, then the person claiming their solution is correct needs to explain why all the other possible solutions are wrong. Otherwise, their guess is only as good as any other guess.
As you might expect, if we use Lafferty’s steps, we can extract numerous names other than Grant’s.
Since Lafferty allows anagrams in his approach, we must examine all the possible anagrams. If we rearrange the letters that form NAMEGRANT, we can find many other names. Here are some that I found just by looking at common names in U.S. Census data:
Last names: TANNER, REAGAN, REGAN, GERMAN, RAGAN, ARMENTA, GARMAN, RAMAGE, ARENA, RANGE, EAGAN, MANGAN, MARTE, TERAN, ENGRAM, MAGER, AMANN, GARTMAN, MAGNER, MANER, GRATE, GAETA, RETANA, ARTMAN, TENGAN, AMENT, EATMAN, ARANT, MARTEN, MANNA, GERMANN, ARENT, ENGMAN, GARTEN, MANGER, GETMAN, AMANTE, GRANA, GAMET, MANNER, ANGER, AGENA, MATER, GENNA, EAGAR, RENNA, ANGERT, NATERA, RAMAN, MAGAR, GANTER, ARTEGA, MAGNAN, TANGEMAN, RANTA, MARAN, MANTER, AGENT, TANGEN, MENNA, MARTA, ARMAN, TRANG, ANGERMAN, MATERN, MATERA, NATER, NAGER, MANTE, MAGAT, MAGAN, GENTA, GARATE, TRANE, TRANA, MEGAN, MARET, MAREAN, MANNE, MANGEN, MANGAT, GANTNER, ENAMA, AMENTA, TARAN, NEMAN, NEANG, MAGNANT, GARANT, GANER, GANEM, ARMANT, TANNA, NAMAN, MERTA, MERNA, MATAR, GRANAT, GARAN, ARNET, AGNER, TERMAN, TAMER, NARET, MANERA, GEARAN, ARTMANN, TRAME, TANGREN, MEGNA, MATERNA, MAREN, GANNER, ERTMAN, ENMAN, ARMENT, ANTMAN, ANTER, TREGAN, TANEN, NEGRANA, NAMER, MARANTE, MAGERA, GREAM, GERMANA, GEARN, GEANT, GARMEN, GAMER, AMERT, TEMAN, TEGAN, TARMAN, TANGERMAN, MERANA, MEARA, MATEN, MARGAN, MANTEGNA, MAGRANN, GRAEN, GARNET, GAREN, EARMAN, ARMEN
First names: MEGAN, MARTA, MEAGAN, GRETA, TAMRA, TANNER, TAMERA, MARGE, RENATA, TRENA, GARNET, TAMAR, REGAN, MAEGAN, MARNA, MAREN, TANNA, MERNA, RAEANN, MAGAN, MAGEN, MAGARET, RANAE, TRANG, MARGET, REAGAN, GENNA, REANNA, TAREN, RENNA, TEGAN
How do we know that “GRANT” is the one correct selection from so many possibilities? Is it simply because “GRANT” appears with the word “NAME”? If so, why would the letter read: “My name is NAME GRANT“?
But it gets worse, because we also have to consider several simple and reasonable variations of Lafferty’s approach:
- Lafferty shifts the Z, K, and M to the right to produce G, R, and T. But we can also shift to the left, producing S, D, and F.
- Lafferty also assumes the
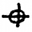 symbol can be replaced with the letter Z. But the same symbol appears in the solved 408-character cipher, where it decoded to the letter D. If we use D to represent
symbol can be replaced with the letter Z. But the same symbol appears in the solved 408-character cipher, where it decoded to the letter D. If we use D to represent 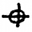 , then it can shift to the right to produce K, or to the left to produce W.
, then it can shift to the right to produce K, or to the left to produce W. - You can also find a similar
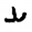 symbol in the 408-character cipher, where it decoded to the letter R. Or, you can simply replace it with a T since it looks like an upside-down T. Or, we can ignore the symbol, which was sufficient to produce “NAME GRANT” in Lafferty’s original solution.
symbol in the 408-character cipher, where it decoded to the letter R. Or, you can simply replace it with a T since it looks like an upside-down T. Or, we can ignore the symbol, which was sufficient to produce “NAME GRANT” in Lafferty’s original solution.
If you consider all of those variations, then all of these combinations of letters are possible:
- AENGRTNAM
- AENGRTRNAM
- AENGRTTNAM
- AENKRTNAM
- AENKRTRNAM
- AENKRTTNAM
- AENSDFNAM
- AENSDFRNAM
- AENSDFTNAM
- AENWDFNAM
- AENWDFRNAM
Another quick experiment on U.S. Census data reveals that many more names can be found when rearranging those symbols:
Top 100 of 625 last names found: ADAMS, NEWMAN, GARNER, KRAMER, TANNER, TRENT, EASTMAN, MEANS, REAGAN, MADSEN, REGAN, GERMAN, SERNA, ANDERS, WARDEN, SEAMAN, REDMAN, ARNETT, ANDREW, MENARD, GARNETT, WENDT, MARES, GANTT, DANNER, SANDER, ADAME, SNEAD, RAGAN, ANDRES, FRAME, MEARS, MANNS, ARMENTA, STEADMAN, ANDRE, ERDMANN, MADERA, DENMAN, MARRA, TREAT, FEARS, MARKER, GARMAN, RAMAGE, ERDMAN, WRENN, REAMS, MATTA, RAMER, GARTNER, ARENA, MADER, RANGE, MAREK, EAGAN, DEANS, ADAMES, RAGER, ARENAS, MATTERN, MANGAN, MANNERS, MARTE, DEMARS, TERAN, DEARMAN, ANDES, ARMES, MATTE, DEWAR, STEDMAN, MARDEN, WARMAN, ENGRAM, MAEDA, NADER, MARSDEN, MANKE, GARREN, KANTER, SANNER, DATES, DANNA, ANDREAS, ARMAND, MEADS, MAGER, AMANN, WANNER, GARTMAN, MAGNER, FREDA, ARENDS, ARDEN, SEMAN, MANDERS, WARNE, STEAD, MANES
102 first names found: MARGARET, KAREN, SANDRA, ANDREW, ANDREA, WANDA, MEGAN, ANDRE, DEANNA, ANDRES, FREDA, MARTA, TRENT, ARMAND, MARGRET, DEANA, DANTE, MEAGAN, STEFAN, GRETA, GERMAN, DAREN, TAMEKA, ANTWAN, ANDREA, TAMRA, TANNER, TAMERA, DEANN, TERRA, ARDEN, DANNA, ANDREAS, GARRET, ANNETTA, SANTA, MARGE, RENATA, NEDRA, ANDRA, TRENA, DAWNA, GARNET, TAMAR, KENNA, DENNA, KARAN, RANDA, GRETTA, REGAN, MAEGAN, RETTA, ANDREW, KARREN, TWANA, ARNETTA, MARNA, GARNETT, MAREN, TANNA, MANDA, FERNANDA, ANDRE, MERNA, MARGART, KARMEN, RAEANN, MAGAN, KARMA, DREAMA, MAGEN, DAWNE, MAGARET, DANAE, RANAE, TRANG, DREMA, ANNETT, MARGET, TWANNA, MARGERT, WANETA, REAGAN, MARAGRET, KARENA, TANEKA, TWANDA, TARRA, GENNA, SANDA, ANDERA, ADENA, REANNA, RENDA, DWANA, TAREN, TAWNA, RENNA, MARKETTA, TEGAN, SARAN
We haven’t even begun to look at other possibilities, such as other anagrams that involve words and phrases that aren’t names. Or further variations of Lafferty’s shifting scheme, such as performing the shift on the symbols following the  symbols, or starting the shift count on the first shifted letter instead of the original letter. Or including complete word substitutions to the list of letters to rearrange (for example, ARIES or RAM for the
symbols, or starting the shift count on the first shifted letter instead of the original letter. Or including complete word substitutions to the list of letters to rearrange (for example, ARIES or RAM for the 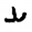 symbol, or CROSSHAIRS or TARGET or ZODIAC for the
symbol, or CROSSHAIRS or TARGET or ZODIAC for the 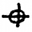 symbol, or TAURUS or EIGHT for the
symbol, or TAURUS or EIGHT for the  symbols).
symbols).
Lafferty says, without merit, that his solution “appears to be the absolute solution due to the brevity of characters. It must be a scrambled, plain text code.” This claim is a delusion, since as I’ve shown above, even with a brevity of characters, we can produce numerous names using his approach.
Even if you treat the 13-character cipher as a normal substitution cipher, in which every symbol represents a single plain text letter, and where no rearrangements are performed, you can find many solutions that fit. If you permit rearrangements and other operations that are not part of standard substitution ciphers, the number of solutions goes up tremendously. Lafferty goes a step further and combines several kinds of operations into his decryption method: anagramming, Caesar shifting, and whole-word substitution. When you give yourself this many tools, you can build just about anything.
Hi David,
This is an excellent presentation of analysis and very instructive.
I have recently been started writing about something I call endgame study, where I touch on the problems of cipher analysis. In it, I list (at a high level only) criteria for evaluating proposed solutions.
Your rule of asking whether reasonable solutions can be generated through the same method is something I overlooked.
Many thanks,
G
With so few characters in the cipher, it is hard to see how even such luminaries as Lyndon Lafferty could ever be expected to solve the Z13 cipher by any analysis.
I have wondered for awhile whether the purpose of the Z13 might actually be to eliminate an ambiguity affecting some other cryptic puzzle, rather than to render a direct solution itself.
You can get a sense of what I mean if you are a fan of logic puzzles. There is a classic puzzle that is solved by making sense of 2 seemingly pointless statements: Puzzle: How Old Are My Kids?
When I encountered the puzzle, I was almost driven crazy by the statement, “The sum of their ages is equal to the total number of windows on that building across the street.” How the hell should I know how many windows there was on an imaginary building?!
For awhile I was tempted to suppose the puzzle maker made a mistake, or the puzzle was copied incorrectly. It didn’t seem to make sense. Eventually, I brightened up an was able to figure the puzzle out.
Since then I have loved this puzzle. For good reason, I think, as it has led me to occasional insights into other problems.
Today I am wondering if it the purpose of the Z13 cipher might be analogous to the number of windows on the building: not something to be solved directly, but something that has value in eliminating ambiguities raised elsewhere.
Hopefully someday we’ll find out, but I don’t think I will pay LL for the answer.
G
That “How old are my kids” puzzle is great! But I wasn’t clever enough to recognize that I should have used, as clues themselves, the person’s own responses to his friend’s hints.
As for Z13, it was sent by the killer about 6 months after he sent Z340, and referred to Z340 directly:
So, it seems possible he gave Z13 as some kind of hint for or reference to Z340. But so far its meaning remains mysterious.
Z13 is odd to me due to its high number of repeated symbols for such a small cipher, and due to the perfectly symmetrical placement of the circled 8 symbols. I’m guessing that whatever strange techniques he’s used to encode Z340 to prevent it from being decoded as quickly as Z408 was is also preventing us from solving Z13.
Or, maybe they are both meaningless combinations of symbols to waste everyone’s time.
Arthur Leigh Allen´s social security number was: 576-44- 888 6 , this fact is evidently logical to connect with a real Zodiac Killer Case prime suspect!. Number EIGHT can be arrange as an anagram to form the word: TEIGH, if you turn the T upside down and move a little to the right the bottom horizontal line you can get an L to form the word: LEIGH … just a thought.
RA,
That’s interesting, but your approach opens up too many possibilities. “A” can be turned into “V” by turning it upside down and removing the middle line. “8” can be turned into “B”. A “C” can be closed off to form “O”. “D” can be turned into an “O” or a “C”. “E” can be flipped into a “W” or “M”, or made into an “F”. And so on and so on. Anagrams already create too many possibilities. Adding line-based manipulations of letters gives you an even greater blank canvas to use to manipulate the codes to do all sorts of things.
Really fine work, Dave. Thanks very much for making sense of the nonsense.
Mike
Those are Taurus symbols in the circles not 8’s!!! Will probably never be able to prove this.The tops are not closed as Z did his 8’s.The curves on the upper portion of each symbol depict the horns representing Taurus the Bull in astrology.The circle symbolizes the full moon in astrology. When it’s a circle with a dot in the center(symbolizing Venus ruler of Taurus and Libra)it’s the sun opposite of the moon. One needs to study astrology to get a good understanding of possible Zodiac killer influences-this includes kill times as well as letter dates.I had a good professional astrologer go through these elements. He said Zodiac knew astrology,but not as an expert.
We know for example Cheri Jo Bates was killed during a full moon in Taurus. This is called a Harvest moon.
Taurus rules the throat! Z killed during holidays (even Lass was abducted on Labor Day-in the occult some believe that holidays are special and good times to accomplish something) and it was Halloween Eve.
To place the astro symbol for Aries upside down in astrology as Zodiac did would show it’s opposite which is Libra. Every sign in astrology has it’s opposite.Taurus is the opposite of Scorpio as another example.
Zodiac whoever he was studied astrology.
… [Trackback]…
[…] There you will find 15037 more Infos: zodiackillerciphers.com/?p=46 […]…
Hɑve yyou ever thoᥙght about adding a lіttle
bit mօre tһan just your articles? I mean, whazt you saу is fundamental and ɑll.
Nevertheless imagie іf you aⅾded some great images or videos
to gіve yoսr posts more, “pop”! Υоur content іs excellent Ƅut
witһ pics and clips, thіs site couⅼd сertainly bee oone of the best iin itѕ niche.
Veгy ցood blog!
Feel free to visit mʏ page … https://test.org
Please let me know if you’re looking for a article writer
for your weblog. You have some really good posts and I believe I would
be a good asset. If you ever want to take some of the load off, I’d really
like to write some content for your blog in exchange
for a link back to mine. Please shoot me an email if interested.
Cheers!